La simulación sencilla que se quiere lograr es simplemente dibujar una figura geométrica de un cilindro en un plano X, Y, dicho plano X, Y representará el área de la malla en la que se estará trabajando, imagine que se quiere dibujar un cilindro en el centro del plano, para proceder con dicha geometría se siguen los pasos sugeridos en el post anterior.
A continuación se muestra la geometría “Cilindro” hecha con C++ y Meep, para ver información sobre esta geometría pero utilizando el lenguaje funcional Scheme favor de visitar el siguiente enlace: http://www.jesusmanzanares.org/manual-del-meep/geometrias/cilindro/
Considere el siguiente diagrama:
Primero que nada se inicializa la función MPI, esto es necesario aunque no se tenga contemplado hacer cálculos en paralelo
cylinder.cpp
meep::initialize mpi(argc, argv); // Do this even for non-MPI Meep
Después, se definen algunas variables de resolución y se define que que se utilizará un PML para el área de frontera de la malla, en esta simulación no es necesario hacer esto pero de todas formas se definirá ya que en la mayoría de las simulaciones se necesitara una condición de frontera que absorba las ondas electromagnéticas
cylinder.cpp
double resolution = 20; // pixels per distance const double pml_thickness = 1.0; const double x = 20 + pml_thickness; const double y = 20 + pml_thickness;
Después, se crea el Volumen que contiene el tamaño de la malla y la resolución y se especifica que el origen de la malla sera exactamente en el centro, esto se tiene que definir de esta forma ya que en C++ el origen por default de la malla se encuentra ubicado en a partir de la parte positiva del plano, es decir, la coordenada 0,0 estará en la esquina izquierda inferior.
cylinder.cpp
grid_volume grid_vol = vol2d(x, y, resolution); // 20x20 2d cell grid_vol.center_origin(); // set the origin as the center of cell
Después, se define la estructura en donde se agrega una referencia al Volumen o malla que se ha creado, también se agrega una referencia con la función que define la geometría que se estará dibujando y por ultimo se le agrega el PML que se definió, esto con la finalidad de definir condiciones de frontera con un material de absorción perfecto aunque esto no es necesario en esta simulación se define por cuestiones ilustrativas ya que la mayoría de las simulaciones contendrán algún tipo de excitación en donde se requerirá contar con un material de absorción en los limites del volumen que nos de la ilusión de continuidad infinita en el campo electromagnético.
cylinder.cpp
structure struct_cylinder(grid_vol, Cylinder, pml(pml_thickness)); // structure cylinder
Después, se define un Field que esta vinculado con la estructura y se agrega una instrucción de optimización, cabe mencionar que esta instrucción de optimización no esta dada por default en Meep C++ contrariamente a lo que ocurre con Scheme.
cylinder.cpp
fields field_cylinder(&struct_cylinder); field_cylinder.use_real_fields(); // this is for optimization purposes
Por último, se define el nombre del archivo en estándar HDF5 a generar, es decir, el archivo en donde se escribirán todos los datos de la simulación en el estándar H5, y se finaliza indicándole a Meep que escriba todos los datos de la simulación en dicho archivo por medio del objeto Field.
cylinder.cpp
h5file *h5_file = field_cylinder.open_h5file("cylinder", h5file::WRITE, "", true);
field_cylinder.output_hdf5(Dielectric, grid_vol.surroundings(), h5_file, false, false, "");
Una de las partes importantes de un programa Meep es la función en donde se definen las geometrías, en este caso la función se ve de la siguiente manera:
cylinder.cpp
double Cylinder(const vec &p) {
double width = 4.0;
double x2 = p.x() * p.x();
double y2 = p.y() * p.y();
double r = sqrt(x2 + y2);
if (r <= width)
return 12.0;
return 1.0;
}
La forma en que la función de la geometría trabaja es la siguiente: Meep hace un barrido internamente punto por punto en donde evalúa si dicho punto se encuentra en la ecuación que se define dentro de esta función, si el punto pertenece al rango de puntos dentro de la función Meep asignara un epsilon de material definido dentro de la condicional, de otra forma Meep asignara el epsilon de material que se le especifique al final de la función, con esta metodología se puede dibujar prácticamente cualquier cosa.
A continuación se enlista el código de la geometría completo:
cylinder.cpp
/*
* _cylinder.cpp
*
* In order to run a simulation using the MEEP C++ interface, the following steps are necessary:
* initialize mpi(argc, argv); // do this even for non-MPI Meep
* create a meep::volume
* create a meep::structure using that volume
* create a meep::fields object
* add some kind of excitation.
* time step the code. Of course, you'll have to create measurements and output whatever data
* you are interested in as well.
*
* Created on: Jul 22, 2011
* Author: yohan
*/
#include <meep.hpp>
#include <iostream>
using namespace meep;
double Cylinder(const vec &p) {
double width = 4.0;
double x2 = p.x() * p.x();
double y2 = p.y() * p.y();
double r = sqrt(x2 + y2);
if (r <= width)
return 12.0;
return 1.0;
}
int main(int argc, char **argv) {
meep::initialize mpi(argc, argv); // Do this even for non-MPI Meep
double resolution = 20; // pixels per distance
const double pml_thickness = 1.0;
const double x = 20 + pml_thickness;
const double y = 20 + pml_thickness;
grid_volume grid_vol = vol2d(x, y, resolution); // 20x20 2d cell
grid_vol.center_origin(); // set the origin as the center of cell
structure struct_cylinder(grid_vol, Cylinder, pml(pml_thickness)); // structure cylinder
fields field_cylinder(&struct_cylinder);
field_cylinder.use_real_fields(); // this is for optimization purposes
h5file *h5_file = field_cylinder.open_h5file("cylinder", h5file::WRITE, "", true);
field_cylinder.output_hdf5(Dielectric, grid_vol.surroundings(), h5_file, false, false, "");
return 0;
}
Para ejecutar la simulación anterior es necesario crear un shell script en donde se especifican algunos paquetes que ayudaran en la conversión de datos en formato HDF5 a formato de imagen así como también hará todo el compilado del código anterior para obtener los resultados deseados, para el caso del bloque y suponiendo que nuestro programa se llama _cylinder.cpp se crea el siguiente archivo bash:
make _cylinder.dac ./_cylinder.dac h5ls cylinder-000000.00.h5 h5topng -Zc dkbluered cylinder-000000.00.h5 rm cylinder-000000.00.h5 rm _cylinder.dac
El shell script anterior compila el programa C++ mediante la instrucción make y crea un archivo de ejecución con extensión “.dac” la cual se ejecuta en la siguiente instrucción, a continuación se utiliza un comando propio de el paquete h5utils desarrollado también por el MIT, el comando h5ls enlista el tamaño del dataset creado que vive en el archivo con extensión H5 y en formato HDF5 este enlistado es solamente con fines informativos. A continuación se ejecuta el comando h5topng el cual como describe su nombre hace una conversión de los datos en formato HDF5 a una imagen en formato PNG, y se finaliza removiendo archivos que ya no serán utilizados al final de la simulación ya que lo que nos interesa por ahora es la imagen.
Para concluir con la ejecución del programa Meep creado, se debe ejecutar el shell script que hará todo el trabajo de escribir todos esos comandos por nosotros con la siguiente instrucción, suponiendo que nuestro script se llame _cylinder.sh.
chmod +x _cylinder.sh sh _cylinder.sh
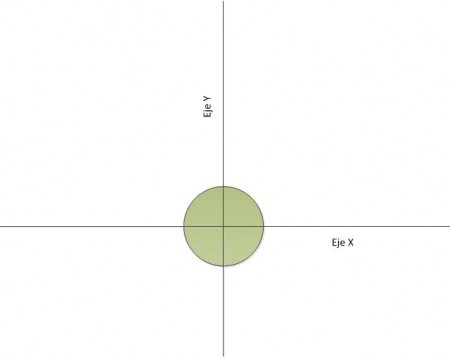
¡Listo!, la simulación nos arrojara el diagrama esperado que se anexa a continuación:
Agregando unos pocos cambios en la función de la geometría se puede obtener un anillo fácilmente:
double Cylinder(const vec &p) {
double width = 2.0;
double inner_radius = 3.0;
double outer_radius = inner_radius + width;
double x2 = p.x() * p.x();
double y2 = p.y() * p.y();
double r = sqrt(x2 + y2);
if ((r > inner_radius) && (r <= outer_radius))
return 12;
return 1.0;
}
Y el resultado se vería de la siguiente manera:
¡Enjoy!